mtmatt.Page

commonPage

0%

發表於 分類於
文章字數： 1.5k 所需閱讀時間 ≈ 3 分鐘

題目連結：AtCoder Beginner Contest 215: D - Coprime 2

題目敘述

給定\(n, m\)下一行會有\(n\)個數字，輸出所有\(k in 1~m\)，\(k\)是與所有數字皆互質的數。

範例輸入 1

1
2
3 12
6 1 5

範例輸出 1

1
2
3
4
3
1
7
11

題解

用埃氏篩法在\(log(n)\) 的時間內做質因數分解，接著將所有數字的質因數聯集存在 bitset 中，最後判斷\(1~m\)的所有數字的質因數之中有無存於 bitset 中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include<bits/stdc++.h>
using namespace std;

using ll=long long;
const ll N=100010;
#define IO_SPEEDUP ios::sync_with_stdio(0);cin.tie(0);
#define IO_INIT cout<<fixed<<setprecision(6);

int n,m;
int pri[N];
bitset<N> bt;

void init(){
    pri[1]=0;
    for(int i=2;i<N;++i){
        if(pri[i]==0){
            pri[i]=i;
            for(ll k=(ll)i*i;k<N;k+=i)
                pri[k]=i;
        }
    }
}

void div(int n){
    while(pri[n]>0){
        bt[pri[n]]=true;
        n/=pri[n];
    }
}

bool check(int n){
    while(pri[n]>0){
        if(bt[pri[n]]){
            return false;
        }
        n/=pri[n];
    }
    return true;
}

int main(){
    IO_SPEEDUP; IO_INIT;

    cin>>n>>m;
    init();

    for(int i=0;i<n;++i){
        int a;
        cin>>a;
        div(a);
    }

    vector<int> ans;
    for(int i=1;i<=m;++i){
        if(check(i)){
            ans.emplace_back(i);
        }
    }

    cout<<ans.size()<<"\n";
    for(auto i:ans){
        cout<<i<<"\n";
    }
}
閱讀全文 »

發表於 分類於
文章字數： 3.5k 所需閱讀時間 ≈ 6 分鐘

前言

我發現，全國能力競賽的難度似乎與我預期的有落差，這一題也是我唯一一個完全解開的題目。真的好難！

題目敘述

「BGP 劫持（BGP Hijacking）」是⼀種透過「邊界閘道器協定（Border Gateway Protocol,BGP）」 的性質進⾏攻擊的⼿段。簡單來說，每個伺服器會宣稱⾃⼰擁有⼀段 IP，並將這個訊息傳遞給周遭的伺服器，來更新他們的路由表。周遭的伺服器也會將這個更新繼續往外傳遞，使伺服器知道要如何將封包傳遞到指定的IP。而 BGP 劫持這個攻擊⼿法，就是透過錯誤地宣稱⾃⼰擁有某⼀段 IP，或者是⾃⼰通往擁有該 IP 的伺服器路徑更短，來使得其他路由器將 IP 往他傳遞。並透過 BGP 更新路由表的特性進⾏⼤規模的流量轉移，使得使⽤者無法存取特定的服務，或者是拿到封包之後拆解其中的內容以獲得敏感資訊。

現在，全國資訊安全能⼒競賽模擬賽要進⾏⼀場 BGP 劫持的攻防⼤賽。這場⽐賽⼀共有 N ⽀隊伍參加，每⽀隊伍會維護⼀台伺服器，之後主辦⽅每次會把⼀個封包丟給⼀個伺服器，並指定他要傳向哪個伺服器。接著每台伺服器會根據他的路由表，選擇⼀個伺服器傳遞封包，而參賽者要做的就是盡可能讓不相關的封包經過⾃⼰，從而破解其中的資訊，而封包的傳遞⽅和接收⽅則要負責保護傳遞的路徑不要被攻擊。作為全國資安第⼀把交椅，翔哥也有關注全國資訊安全能⼒競賽模擬賽，但是翔哥真的太強了，這種⽐賽的勝敗他並不放在⼼上，他關⼼的是有沒有可能⼤家都享受到⽐賽的過程。雖然傳遞的路徑會根據路由表以及接收者而異，可是這對翔哥來說是 a piece of cake。他已經預測出了 M 個封包潛在被劫持的⽅式。根據封包傳遞的性質，這些路徑必定不會讓封包在數個隊伍之間循環傳遞。

現在，翔哥想知道是否存在⼀種 BGP 劫持的狀況，使得封包會經過每⽀隊伍恰好⼀次。

輸入說明

輸⼊的第⼀⾏包含兩個⾮負整數 N 、M ，代表全國資訊安全能⼒競賽模擬賽⼀共有 N 個隊伍參加，且 有 M 個可能的封包劫持狀況。 接下來的 M ⾏，每⾏包含兩個正整數 si、ti，代表第 si 個隊伍拿到的封包有可能被第 ti 個隊伍劫持。 保證不存在⼀種劫持路徑使得⼀個封包可以在數個隊伍之間循環傳遞。

輸出說明

如果存在⼀種劫持封包的⽅式，使得每個隊伍會接⼿那個封包恰好⼀次，請輸出 N 個正整數於⼀⾏，代表封包可以依序經過哪些隊伍的伺服器，否則請輸出 −1。如果有很多種封包傳遞路徑都滿⾜條件，輸出任意⼀個都可以獲得 Accepted。

閱讀全文 »

發表於 分類於
文章字數： 3.9k 所需閱讀時間 ≈ 7 分鐘

題目連結：1143 - 4.靈犬尋寶 | TIOJ INFOR Online Judge

題目敘述

正方形(左下角座標為(0,0)，右上角座標為(99,99))的格網上，有一隻靈犬要尋找一個寶物，格網上除了靈犬與寶物之外，還有一些障礙物。一般情況下，只要不超出格網的邊界，靈犬的每一步最多有 8 個方向可供選擇，如圖一；但是必須注意，只有在 A 點沒有障礙物時才可以選擇方向 1 或方向 2，只有在 B 點沒有障礙物時才可以選擇方向 3 或方向 4，只有在 C 點沒有障礙物時才可以選擇方向 5 或方向 6，只有在 D 點沒有障礙物時才可以選擇方向 7 或方向 8。如果靈犬可以從出發的位置走到寶物的位置，其總共使用的步數，理論上應有一個最小值；但是靈犬也有可能無法走到寶物的位置。過程中，靈犬不可以走到障礙物的位置上。

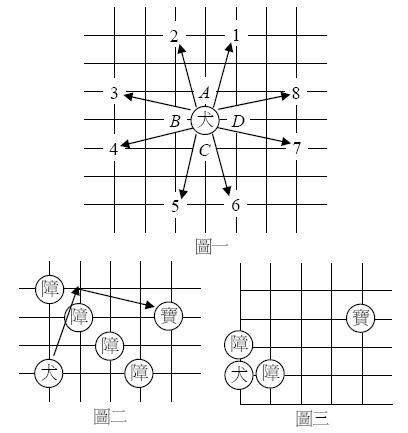
以圖二為例，有多達 4 個障礙物介於靈犬與寶物之間，但是靈犬最快只要 2 步就可以到達寶物的位置。圖三是另一個例子，靈犬的位置靠近角落，雖然只有 2 個障礙物，靈犬卻無法到達寶物的位置。

請撰寫一個程式，若靈犬可以從最初位置走到寶物的位置時，請列印出其使用之最少步數；若靈犬無法到達寶物的位置，請列印出單字 “\(impossible\)”。

輸入說明

第一行為一個整數 \(n\)，代表障礙物的個數，\(0 \le n \le 1000\)。接下來的\(n\)行，每行表示一個障礙物的座標，其橫座標值與縱座標值間以一個空白隔開。 再下來的一行，表示靈犬的最初位置，其橫座標值與縱座標值間以一個空白隔開。 最後一行，代表寶物的位置，其橫座標值與縱座標值間以一個空白隔開。 注意：輸入之障礙物、靈犬、寶物皆在不同位置。所有橫、縱座標值均為介於 \(0\)(含)至\(99(含)\) 之間的整數。

輸出說明

依行走之規則，若靈犬可以從其位置走到寶物的位置時，請列印出其使用之最少步數；若靈犬無法到達寶物的位置，請列印出單字 “\(impossible\)”。

閱讀全文 »

發表於 分類於
文章字數： 2.7k 所需閱讀時間 ≈ 5 分鐘

題目連結：1142 - 3.關鍵邏輯閘 | TIOJ INFOR Online Judge

題目敘述

一個組合電路(combinational circuit)由線路(wires)連接一組邏輯閘(logic gates)而成，並且不包含有向迴路(directed cycle)。一個組合電路的效能決定於最後一個主要輸出(primary output)被算出來的時間。假設每一個邏輯閘所需的運算時間都是固定並且是已知的，而線路的延遲(delay)是 0。我們希望把一個組合電路所有的關鍵邏輯閘找出來。若一個邏輯閘的運算時間有任何延長，便會影響到整個電路的效能，它就被稱為關鍵邏輯閘。以圖一的組合電路為例，I1、I2、I3 是主要輸入；O1、O2 是主要輸出；圓圈代表邏輯閘，箭頭代表線路；每個邏輯閘有自己的編號以及固定的延遲時間。在圖一的例子當中，該組合電路中的 O1 會因為邏輯閘 2、4、5 的延遲，在時間 400 才會收到運算結果；而 O2 會因為邏輯閘 2、4、6 的延遲，在時間 600 才收到運算結果，因此 O2 是最後一個被算出來的主要輸出。關鍵邏輯閘分別是 2、4 以及 6 號邏輯閘，當其中一個關鍵邏輯閘的運算時間有任何延長，O2 被算出來的時間也會再往後延遲。相反地，就算 1 號邏輯閘的運算時間從 150 延長到 160，也不會影響到 O2 被算出來的時間，因此 1 號邏輯閘並不是關鍵邏輯閘。

輸入說明

第一行為一個整數 \(n (0 < n < 10000)\)，代表一個組合電路的邏輯閘總數，每個邏輯閘的編號都不同，且範圍是介於 \(1,2,…n\) 之間的整數。第二行為一個整數 \(m (m < 50000)\)，代表線路的總數。接下來的 \(n\) 行，依序列出每個邏輯閘的運算時間；每個運算時間的值是介於 0 到 600 之間(含)的整數。最後 \(m\) 行，分別列出每一條線路由某個邏輯閘的輸出接到另一個邏輯閘的輸入。 注意：為簡化輸入，我們把主要輸入(primary inputs)與邏輯閘之間的線路，以及邏輯閘與主要輸出(primary outputs)之間的線路省略。(每一個邏輯閘至少都含有一個線路輸出到另一個邏輯閘或主要輸出)

輸出說明

列出關鍵邏輯閘的個數。

範例輸入 1

1
2
3
4
5
6
7
8
9
10
5 4
200
200
400
250
200
1 2
3 2
3 5
4 5

範例輸出 1

閱讀全文 »

發表於 分類於 ，
文章字數： 759 所需閱讀時間 ≈ 1 分鐘

1. 對聯

  • A : 2, 4字平仄不同 && 2, 6平仄相同
  • B : 第一句最後一字仄，第二句則是平
  • C : 第一二句2, 4, 6 字分別平仄不同

input : 七言對聯 0->平, 1->仄

1
2
3
1
0 0 0 0 1 1 1
1 1 1 1 0 0 0

ouput : 違反ABC哪些個規則就輸出相對應的英文字母(ABC)，若沒違反則輸出 “None”

1
A

2. 炸彈魔王

遊戲採回合制，回合開始時若魔王位於炸彈上則所有在同一格的魔王會連同炸彈一起消失，所有未消失的魔王會先在腳下放一顆炸彈，再依據方向向量(s, t)移動。移動到邊界外的魔王視為消失。 求所有魔王消失時還有未爆彈的地點數。

n,m,r,c <= 100, k<500, |s,t|<=10

input : 第一行 n, m, k 分別表示地圖長寬以及魔王數，接下來有 k 行每一行都有 r, c, s, t 分別表示魔王初始位置座標，以及移動向量。

閱讀全文 »

發表於 分類於
文章字數： 6k 所需閱讀時間 ≈ 11 分鐘

Binary Search Tree (二元搜尋樹)，是用來存放多筆資料，並快速搜尋的資料結構。大概的原則就是，大的放右邊，小的放左邊。

新增，刪除一個值都只要 \(O(log(N))\)

以下為實作範例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
#include
using namespace std;

template
class bst{
    private:
        struct node{
            T val;
            node* l,r;

            node(){
                l=r=nullptr;
            }
            node(T v){
                l=r=nullptr;
                val=v;
            }
        };

        bool find(node *n,T v){
            if(n->val==v){
                return true;
            }else if(n->val > v && n->r!=nullptr){
                find(n->r,v);
            }else if(n->val < v && n->l!=nullptr){
                find(n->l,v);
            }else{
                return false;
            }
        }

        void insert(node *&n,T v){
            if(n==nullptr){
                node nd=new node(v);
                n=&nd;
            }else if(n->val > v && n->r!=nullptr){
                insert(n->r,v);
            }else if(n->val < v && n->l!=nullptr){
                insert(n->l,v);
            }
        }

        void DeleteNode(node *&n){
            if(n->l==nullptr && n->r==nullptr){
                delete n;
                n=nullptr;
            }else{
                node *left,*right;
                if(n->l==nullptr){
                    right=n->r;
                    n->val=right->val;
                    n->l=right->l;
                    n->r=right->r;
                    delete right;
                }else if(n->r==nullptr){
                    left=n->l;
                    n->val=left->val;
                    n->l=left->l;
                    n->r=left->r;
                    delete left;
                }else{
                    right=n;
                    left=n->l;
                    while(left->r!=nullptr){
                        right=left;
                        left=left->l;
                    }
                    n->val=left->val;
                    if(right!=n)
                        right->r=left->l;
                    else
                        right->l=left->l;
                    delete left;
                }
            } 
        }

        void erase(node *n,T v){
            if(n->val==v){
                DeleteNode(n);
            }else if(n->val > v && n->r!=nullptr){
                erase(n->r,v);
            }else if(n->val < v && n->l!=nullptr){
                erase(n->l,v);
            }
        }

        void DeleteTree(node *n){
            if(n->l!=nullptr)
                DeleteTree(n->l);
            if(n->r!=nullptr)
                DeleteTree(n->r);
            delete n;
        }
    public:
        bst(){
            root=nullptr;
            sz=0;
        }

        ~bst(){
            if(root!=nullptr)
                DeleteTree(root);
        }

        bool find(T v){
            if(root!=nullptr)
                return find(root,v);
        }

        void insert(T v){
            if(root==nullptr){
                node n=new node(v);
                root=&n;
            }else{
                insert(root,v);
            }
            sz++;
        }

        void erase(T v){
            if(root==nullptr) return;
            erase(root,v);
            sz--;
        }

        int size(){
            return sz;
        }
    private:
        node *root;
        int sz;
};

相同的，C++都幫你做好了，就是所謂的Set & Map。

以下為使用範例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include
using namespace std;

int main(){
    vector v(100);
    for(int i=0;i<100;++i){
        v[i]=i;
    }
    random_shuffle(v.begin(),v.end());

    set s;
    for(auto a:v){
        s.insert(a);
    }

    random_shuffle(v.begin(),v.end());

    for(auto a:v){
        cout<<*s.lower_bound(a)<<" ";
        cout<<*s.upper_bound(a)<<"\n";
    }
    s.erase(10);
    cout<<*s.lower_bound(10);
}

我相信許多人跟我一樣，一開始不知道這些東西要用在哪？

以下我找了幾個範例

1. 在O(Nlog(26))以內找出是否有一個字母在兩個字串中均能被找到(題目連結：Two Strings | HackerRank)

閱讀全文 »

發表於 分類於
文章字數： 4.5k 所需閱讀時間 ≈ 8 分鐘

Stack，又稱作堆疊，顧名思義就是從上面(也可以說前面)放入與取出的資料結構。 Queue，稱為佇列，是從前面放後面取出的資料結構。

實作程式碼如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include<bits/stdc++.h>
using namespace std;

template<class T>
class Stack{
    private:
        int t=-1;
        vector<T> dt;
    public:
        T top(){
            if(t!=-1){
                return dt[t];
            }else{
                cout<<"Stack is empty.\n";
            }
        }

        void pop(){
            if(t!=-1){
                t--;
                dt.pop_back();
            }else{
                cout<<"Stack is empty.\n";
            }
        }

        void push(T p){
            t++;
            dt.push_back(p);
        }
};

template<class T>
class Queue{
    private:
        deque<T> dt;
    public:
        T front(){
            if(!dt.empty()){
                return dt.front();
            }else{
                cout<<"Queue is empty.\n";
            }
        }

        void pop(){
            if(!dt.empty()){
                dt.pop_front();
            }else{
                cout<<"Queue is empty.\n";
            }
        }

        void push(T p){
            dt.push_back(p);
        }
};

C++已經幫你將這兩個資料結構實做好了，以下示範例程式碼

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<iostream>
#include<stack>
#include<queue>
#include<deque>

using namespace std;

int main(){
    stack<int> st;
    for(int i=0;i<10;++i){
        st.push(i);
    }
    cout<<st.size()<<"\n";
    while(!st.empty()){
        cout<<st.top()<<" ";
        st.pop();
    }
    cout<<"\n\n";

    queue<int> q;
    for(int i=0;i<10;++i){
        q.push(i);
    }
    cout<<q.size()<<"\n";
    while(!q.empty()){
        cout<<q.front()<<" "<<q.back()<<"\n";
        q.pop();
    }
    cout<<"\n";
}

光聽這兩個介紹以及大部分的分享，相信你還是不知道這兩個東西要用在哪裡。以下會有幾個應用的範例，都是用 STL 。

1.在 O(N) 的複雜度下做單調對列 Ex : 洛谷

題目敘述： 對於每個元素，從後面找出第一個比他大的元素的位置

這題就是要透過 stack 保持裡面所存位置對應的元素的單調遞減性。實際做法就是，遇到比他大的就丟掉，反正已經確認現在這個元素已經比他大了，後面也不會用到。否則他就還沒遇到還沒遇到比他大的。

以下為程式碼

閱讀全文 »