mtmatt.Page

commonPage

0%

TIOJ 1143 95_4.靈犬尋寶

發表於 分類於
文章字數： 3.9k 所需閱讀時間 ≈ 7 分鐘

題目連結：1143 - 4.靈犬尋寶 | TIOJ INFOR Online Judge

題目敘述

正方形(左下角座標為(0,0)，右上角座標為(99,99))的格網上，有一隻靈犬要尋找一個寶物，格網上除了靈犬與寶物之外，還有一些障礙物。一般情況下，只要不超出格網的邊界，靈犬的每一步最多有 8 個方向可供選擇，如圖一；但是必須注意，只有在 A 點沒有障礙物時才可以選擇方向 1 或方向 2，只有在 B 點沒有障礙物時才可以選擇方向 3 或方向 4，只有在 C 點沒有障礙物時才可以選擇方向 5 或方向 6，只有在 D 點沒有障礙物時才可以選擇方向 7 或方向 8。如果靈犬可以從出發的位置走到寶物的位置，其總共使用的步數，理論上應有一個最小值；但是靈犬也有可能無法走到寶物的位置。過程中，靈犬不可以走到障礙物的位置上。

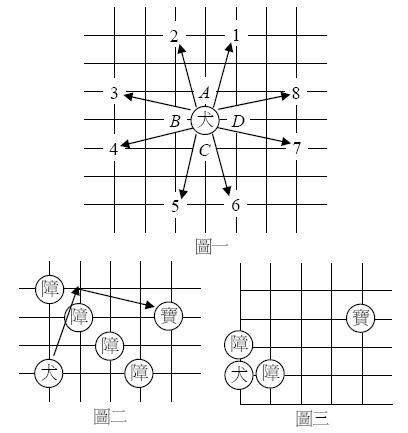
以圖二為例，有多達 4 個障礙物介於靈犬與寶物之間，但是靈犬最快只要 2 步就可以到達寶物的位置。圖三是另一個例子，靈犬的位置靠近角落，雖然只有 2 個障礙物，靈犬卻無法到達寶物的位置。

請撰寫一個程式，若靈犬可以從最初位置走到寶物的位置時，請列印出其使用之最少步數；若靈犬無法到達寶物的位置，請列印出單字 “\(impossible\)”。

輸入說明

第一行為一個整數 \(n\)，代表障礙物的個數，\(0 \le n \le 1000\)。接下來的\(n\)行，每行表示一個障礙物的座標，其橫座標值與縱座標值間以一個空白隔開。 再下來的一行，表示靈犬的最初位置，其橫座標值與縱座標值間以一個空白隔開。 最後一行，代表寶物的位置，其橫座標值與縱座標值間以一個空白隔開。 注意：輸入之障礙物、靈犬、寶物皆在不同位置。所有橫、縱座標值均為介於 \(0\)(含)至\(99(含)\) 之間的整數。

輸出說明

依行走之規則，若靈犬可以從其位置走到寶物的位置時，請列印出其使用之最少步數；若靈犬無法到達寶物的位置，請列印出單字 “\(impossible\)”。

範例輸入 1

1
2
3
4
5
6
7
4
3 6
4 5
5 4
6 3
3 3
7 5

範例輸出 1

1
2

範例輸入 2

1
2
3
4
5
2
1 1
0 2
0 1
4 3

範例輸出 2

1
impossible

題解

這很明顯是圖的 BFS，而為何不是 DFS 呢？因為題目要求輸出最短的路徑，而在 DFS 的時候，只要下一步能走就一直走，因此不一定會是最短路徑。

在 BFS 時，要先判斷座標是否存在，再看是否會被阻擋，以及是否已經到過，最後還有目標位置有無障礙物。若以上條件均通過才能將他推入佇列。

實作程式碼如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
#include<bits/stdc++.h>
using namespace std;
//這樣在宣告 long long 時可以用 ll 代替
using ll=long long;
//常數 N 表示最大地圖長寬，多 5 以求保險
const ll N=105;

//位置
struct Pos{
    int r,c;

    friend bool operator==(Pos a,Pos b){
        return (a.r==b.r && a.c==b.c);
    }

    void operator+=(Pos b){
        r+=b.r;
        c+=b.c;
    }
};

//位置變化量
struct Deg{
    Pos pos;
    Pos lmt;
};

const Deg d[8]={
    {Pos{ 3, 1},Pos{ 1, 0}},
    {Pos{ 3,-1},Pos{ 1, 0}},
    {Pos{ 1,-3},Pos{ 0,-1}},
    {Pos{-1,-3},Pos{ 0,-1}},
    {Pos{-3, 1},Pos{-1, 0}},
    {Pos{-3,-1},Pos{-1, 0}},
    {Pos{-1, 3},Pos{ 0, 1}},
    {Pos{ 1, 3},Pos{ 0, 1}}
};

int n;

void solve(){
//  mp 存那些位置有障礙物
    bitset<N> mp[N];
    int ct[N][N]={0};

    for(int i=0;i<n;++i){
        int r,c;
        cin>>r>>c;
        mp[r][c]=true;
    }

    Pos pos,loot;
    cin>>pos.r>>pos.c;
    cin>>loot.r>>loot.c;

    if((abs(pos.r-loot.r)+abs(pos.c-loot.c)) & 1){
        cout<<"impossible"<<"\n";
        return;
    }

    bool isf=false;
//  初始化
    queue<Pos> bfs;
    bfs.push(pos);
//  用 1 初始化避免以為沒到過
    ct[pos.r][pos.c]=1;

    while(!bfs.empty()){
        Pos now=bfs.front();
        bfs.pop();

        if(now==loot){
//          因為初始化為 1，因此就要將答案 -1
            cout<<ct[now.r][now.c]-1<<"\n";
            isf=true;
            break;
        }

        for(int i=0;i<8;++i){
            Pos next=now;
            next+=d[i].pos;
//          座標存在與否
            if(next.r<100 && next.c<100 && next.r>=0 && next.c>=0){
//              目標位置有無障礙物
                if(!mp[next.r][next.c]){
//                  是否會被阻擋
                    if(!mp[now.r+d[i].lmt.r][now.c+d[i].lmt.c]){
//                      是否已經到過
                        if(!ct[next.r][next.c]){
                            bfs.push(next);
                            ct[next.r][next.c]=ct[now.r][now.c]+1;
                        }
                    }
                }
            }
        }
    }

    if(!isf){
        cout<<"impossible"<<"\n";
    }
}

int main(){
    ios::sync_with_stdio(0);cin.tie(0);
//處理多筆輸入 (用於ZeroJudge:b059)，但單筆輸入也不會錯
    while(cin>>n){
        solve();
    }
}