mtmatt.Page

commonPage

0%

TIOJ 1142 95_3.關鍵邏輯閘

發表於 分類於
文章字數： 2.7k 所需閱讀時間 ≈ 5 分鐘

題目連結：1142 - 3.關鍵邏輯閘 | TIOJ INFOR Online Judge

題目敘述

一個組合電路(combinational circuit)由線路(wires)連接一組邏輯閘(logic gates)而成，並且不包含有向迴路(directed cycle)。一個組合電路的效能決定於最後一個主要輸出(primary output)被算出來的時間。假設每一個邏輯閘所需的運算時間都是固定並且是已知的，而線路的延遲(delay)是 0。我們希望把一個組合電路所有的關鍵邏輯閘找出來。若一個邏輯閘的運算時間有任何延長，便會影響到整個電路的效能，它就被稱為關鍵邏輯閘。以圖一的組合電路為例，I1、I2、I3 是主要輸入；O1、O2 是主要輸出；圓圈代表邏輯閘，箭頭代表線路；每個邏輯閘有自己的編號以及固定的延遲時間。在圖一的例子當中，該組合電路中的 O1 會因為邏輯閘 2、4、5 的延遲，在時間 400 才會收到運算結果；而 O2 會因為邏輯閘 2、4、6 的延遲，在時間 600 才收到運算結果，因此 O2 是最後一個被算出來的主要輸出。關鍵邏輯閘分別是 2、4 以及 6 號邏輯閘，當其中一個關鍵邏輯閘的運算時間有任何延長，O2 被算出來的時間也會再往後延遲。相反地，就算 1 號邏輯閘的運算時間從 150 延長到 160，也不會影響到 O2 被算出來的時間，因此 1 號邏輯閘並不是關鍵邏輯閘。

輸入說明

第一行為一個整數 \(n (0 < n < 10000)\)，代表一個組合電路的邏輯閘總數，每個邏輯閘的編號都不同，且範圍是介於 \(1,2,…n\) 之間的整數。第二行為一個整數 \(m (m < 50000)\)，代表線路的總數。接下來的 \(n\) 行，依序列出每個邏輯閘的運算時間；每個運算時間的值是介於 0 到 600 之間(含)的整數。最後 \(m\) 行，分別列出每一條線路由某個邏輯閘的輸出接到另一個邏輯閘的輸入。 注意：為簡化輸入，我們把主要輸入(primary inputs)與邏輯閘之間的線路，以及邏輯閘與主要輸出(primary outputs)之間的線路省略。(每一個邏輯閘至少都含有一個線路輸出到另一個邏輯閘或主要輸出)

輸出說明

列出關鍵邏輯閘的個數。

範例輸入 1

1
2
3
4
5
6
7
8
9
10
5 4
200
200
400
250
200
1 2
3 2
3 5
4 5

範例輸出 1

1
3

題解

很明顯，題目是要最長的路徑，因為最後一個完成的才會是關鍵邏輯閘，並且圖是有向無環圖，我的想法是先做出反圖( f->t 存成 t->f )，接著將所有終點接到虛擬點 0，並用一次 DFS 算出所有點的最長路徑。以範測為例。

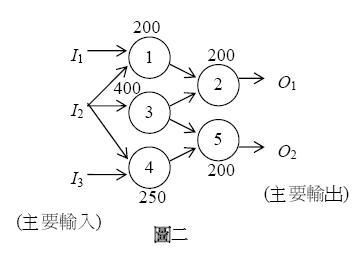
原圖的邊有 1->2, 3->2, 3->5, 和 4->5。我將它存為下圖

TIOJ1142_p1

可以聲稱一個性質 “對於每個點而言，只有反圖上累積路徑最長的那幾條，後面的點才會有可能是關鍵邏輯閘”，最後再做一次 DFS ，知道那些點是關鍵就可以間接算出數量了。

實作程式碼如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include<bits/stdc++.h>
using namespace std;

using ll=long long;
const ll N=10010;

int n,m;
//dis存運算時間，dp 存到這個點的最長距離
int dis[N],dp[N];
//ind表示 indegree，ind[i] 為零的都是終點
int ind[N];
//圖的鄰接串列表示法
vector<int> g[N];
//哪些是關鍵
bitset<N> ans;

//第一次 DFS
void init(int node){
    dp[node]=0;
    for(auto i:g[node]){
        init(i);
        dp[node]=max(dp[node],dp[i]);
    }
    dp[node]+=dis[node];
}

//第二次 DFS
void dfs(int node){
    int mx=0;
    bitset<N> tp;
    for(auto i:g[node]){
        if(dp[i]>mx){
            tp.reset();
            mx=dp[i];
            tp[i]=true;
        }else if(dp[i]==mx){
            tp[i]=true;
        }
    }

    for(auto i:g[node]){
        if(tp[i]){
            dfs(i);
        }
    }
    ans|=tp;
}

int main(){
    ios::sync_with_stdio(0);cin.tie(0);

    cin>>n>>m;
    for(int i=1;i<=n;++i){
        cin>>dis[i];
    }

    for(int i=0;i<m;++i){
        int f,t;
        cin>>f>>t;
        g[t].emplace_back(f);
        ind[f]++;
    }

//  將所有終點用點 0 連接
    for(int i=1;i<=n;++i){
        if(ind[i]==0){
            g[0].emplace_back(i);
        }
    }

//  最後各跑一次就可以求出答案了
    init(0);
    dfs(0);

    cout<<ans.count();
}