mtmatt.Page

commonPage

0%

APCS 講義

發表於 分類於 ，
文章字數： 24k 所需閱讀時間 ≈ 43 分鐘

源起 & 說明

起心動念編纂這本「講義」的時候，正值我準備 APCS 考試期間，當時也正在就讀高中，考量到時間上的不足，我邀請 3 個人一起參與，所以，作者總共有 4 個人，而本篇貼文所摘錄的是我所創作的部分。

作者序

演算法與資料結構一直以來都是程式設計中最重要的部分。然而許多的書籍在介紹時，出於篇幅考量，字句精簡，以致晦澀難懂。本書旨在對於演算法及資料結構進行詳細的介紹，避免初學者遇到與我相同的困境，因而花費許多時間。雖說是競賽入門，然我仍有計畫放一些進階的資料結構與演算法。

後續我盡可能會將所有題目放在 ZeroJudge 的課程裡，方便大家測試自己的程式碼，也方便除錯。
(參加課程方式。從使用者選單->「參加課程」->課程代碼：a7HcCs)

這本書作為我程式設計學習的其中一個指標，也是我自主學習計畫的內容。希望能幫助到一些在資料結構與演算法的學習與運用上不知如何進展的人。

作者：李尚哲、余光磊、戴偉璿與李卓岳。

本教材歡迎分享使用，僅須註明出處，惟不得作營利用途。

樹狀樹組-BIT

快速求取區間和的助手

回顧

還記得前綴和嗎，他也是用來求區間和的，但你應該會發現，若當中有一個值需要被修改，那整列都會被動到。

以下是一個比較表，了解BIT強大之處

資料結構 查尋區間和 單點修改值
純陣列 \(O(n)\) \(O(1)\)
前綴和 \(O(1)\) \(O(n)\)
BIT \(O(log(n))\) \(O(log(n))\)

用途 & 概念

BIT用於在快速求取區間和的同時，又能保證快速修改。感覺像是陣列與前綴和的優點結合下的產物，不過其複雜程度也是三者之中最高的。以下為示意圖，其中數字代表它儲存的區間。

myApcsHanoutEp1

如果想要知道1~5的和，可以查詢1~4+5。以下為查詢所需區間表。

1 1~2 1~3 1~4 1~5 1~6 1~7 1~8
1 1~2 1~2 & 3 1~4 1~4 & 5 14 & 56 14 & 56 & 7 1~8

可以發現，在元素數量為8時，最多會需要查詢3個區間就可以得到1~n的值，接著就像前綴和那樣，用1~R - 1~(L-1)就可以求出所有區間的和了。

實作

BIT一般都是用陣列實作，用區間最大值作為存放位置(例如1~4放在4)。那搜尋與修改呢？這部分就比較複雜了，需要了解一些二進位制，如果你已經理解二進位制了，那就繼續往下看吧。

二進位表

1 2 3 4 5 6 7 8
000001 000010 000011 000100 000101 000110 000111 001000

lowbit

lowbit是在二進位下右邊看過來最前面的1，例如：6(000110)就是2(000010)，一樣提供一個表

1 2 3 4 5 6 7 8
000001 000010 000011 000100 000101 000110 000111 001000
000001 000010 000001 000100 000001 000010 000001 001000

查詢

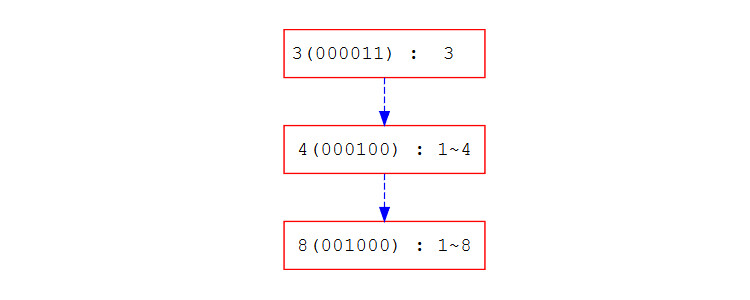
可以發現，\(x\)重複\(-lowbit(x)\)會變成0，且途中會經過所有需要的區間。以7為例

myApcsHanoutEp2

只要將所有經過的區間加在一起，就可以得到區間和了。這也呼應為何他查尋的複雜度為\(O(log(n))\)，因為\(n\)只會有\(log(n)\)個\(bit\)。

修改

myApcsHanoutEp3

這樣最多也是\(O(log(n))\)。也可以發現\(lowbit\)的重要性。

程式碼

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<bits/stdc++.h>
using namespace std;

#define lowbit(x) (x&-x)
// 與 int lowbit(x){ return x&-x;}
// 用define或函式雖然不會讓你的程式碼寫起來比較快，但可以使其較易於理解。

using ll=long long;

ll bt[200010];
ll a[200010];

// build 函式是透過逐個更新陣列的所有元素來建構BIT
void build(int n){
    for(int i=1;i<=n;++i)
        for(int x=i;x<200005;x+=lowbit(x))
            bt[x]+=a[i];
}

// 單點加值
void add(int x,int k){
    a[x]+=k;
    for(int i=x;i<=200005;i+=lowbit(i))
        bt[i]+=k;
}

// 由單點加值衍生出來的單點修改
void modify(int x,int k){
    add(x,k-a[i]);
}

// 搜尋1~x的區間和
ll find_sum(int x){
    ll ret=0;
    for(int i=x;i>0;i-=lowbit(i))
        ret+=bt[i];
    return ret;
}

// 用計算(1~r) - (1~(l-1))算出所有區間的區間和
ll query(int l,int r){
    return find_sum(r)-find_sum(l-1);
}

習題

Q-13-1 區域調查(POJ.1195 Mobile phones 改編)

題目敘述 :

給一個矩陣 T(1,1), T(1,2),…. T(N,M)，求 T(x1,y1) 到 T(x2,y2) 的總和 或者是修改 T(x1,y1) 的值

輸入說明 :

每組輸入的第一行會有兩個正整數 N Q ( 1 ≦ N ≦ 250, Q ≦ 50,0000)

接下來會有 N 行，每行上會有 N 個元素 M ( 0 ≦ M ≦ 32767 )

接下來會有 Q 行，倘若第一個數字為 1，則接下來會有四個數字

x1 , y1 , x2 , y2， 1 ≦ x1 , y1 , x2 , y2 ≦ 250

請輸出元素 \(S={( x , y ) | x1 ≦ x ≦ x2, y1 ≦ y ≦ y2 }\)符合的所有元素總和

倘若第一個數字為2，則接下來會有三個數字

x1 , y1 , V， 1 ≦ x1 , y1 ≦ 250 , 0 ≦ V ≦ 32767,

請修改 ( x1 , y1 )= V ; 此行不必輸出

輸出說明 :

若為調查，則輸出區域中的元素總和，若為修改，則不必輸出

範例輸入 1 :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5 10
3 2 2 3 7
4 4 0 3 8
2 4 7 2 3
5 9 6 1 4
7 1 7 1 1
2 2 2 1
1 5 4 5 5
2 2 1 7
1 3 2 1 5
1 2 5 4 5
1 1 2 2 1
2 2 2 7
2 4 5 5
1 3 3 4 5
1 4 3 2 2

範例輸出 1 :

1
2
3
4
5
6
2
42
15
13
24
33

Q-13-2 2D rank finding problem(98學年度中投區資訊學科能力競賽)

題目敘述 :

二度空間上的排名計算問題(2D rank finding problem)：給定二度平面空間(2D)上的點A = (a1,a2)與點B = (b1,b2)，其大小關係定義為若A > B 若且唯若 a1> b1 且 a2 > b2 ;亦即A點在B點的右上方。如下圖中，B >A, C>A, D>A, D>C, D> B。值得注意的是，並非任意兩點均可以決定大小關係，如下圖中的點A與點E，點D與點E等，無法決定這兩點的大小關係故為無法比較(incomparable)。給定N個點(x1,y1), (x2,y2), …, (xn,yn)，定義某一個點的排名(rank) 為所給的點集合中，比該點小的點的個數。

設計一個程式，從檔案讀取點的名稱與座標，計算出在所給定的集合中，所有點的排名值。

輸入說明 :

有多組測試資料

每組的第一行有一個數字N ( 1 ≦ N ≦ 10000 )

接下來會有N行，每行上會有兩個數字 x y ( 1 ≦ x , y ≦ 1000 )

輸出說明 :

請按照輸入的順序，求出對於 ( x , y ) 有多少個點 ( a , b )

在它的左下方 a < x , b < y

範例輸入 1 :

1
2
3
4
5
6
5
961 404
640 145
983 888
539 71
437 532

範例輸出 1 :

1
2
3
4
5
2
1
4
0
0

Q-13-3 低地距離(2020年10月APCS)

題目敘述 :

輸入一個長度為 2n 的陣列，其中 1 ~ n 的每個數字都剛好各 2 次。

i 的低窪值的定義是兩個數值為 i 的位置中間，有幾個小於 i 的的數字。

以 \([3, 1, 2, 1, 3, 2]\) 為例，1的低窪值為 0, 2 的低窪值值為 1, 3 的低窪值為 3。

請對於每個 1 ~ n 的數字都求其低窪值（兩個相同的數字之間有幾個數字比它小），輸出低窪值的總和，答案可能會超過 C++ int 的上限。

輸入說明 :

第一行有一個正整數 n
第二行有 2n 個正整數，以空格分隔，保證 1 ~ n 每個數字都恰好出現兩次。

1≤n≤100000

輸出說明 :

輸出 1 ~ n 每個數字的低窪值總和。

範例輸入 1 :

1
2
3
3 1 2 1 3 2

範例輸出 1 :

1
4

線段樹

於競賽而言強大的工具。

用法 & 概念

線段樹除了可以用來快速解區間和問題，還可以用來執行許多與區間有關的操作。大致上用以下方式建構區間

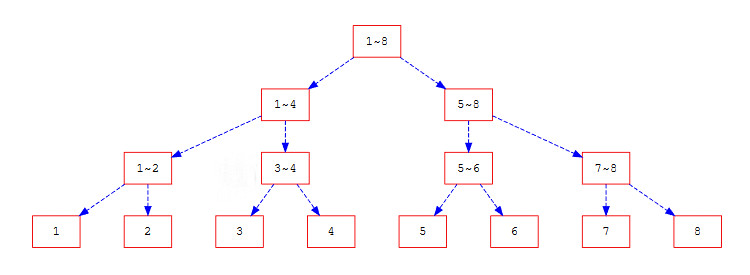
myApcsHanoutEp4

每個區間視情況放不同的數值，例如：最大/小，或是區間總和等。

接著，每個區間就都可以分為\(O(log(n))\)個區間，例如2~7可以分為2, 3~4, 5~6, 7

myApcsHanoutEp5

查詢時皆以最大區間為出發點，例如上圖就會是從1~8這個區間開始，如果要查詢的區間是2~7。因為1~8這個區間並沒有完全包含2~7，因此需要往下遞迴，分成1~4和5~8再次查詢。

接著，因為1~4和5~8仍然沒有完全被2~7包含，因此要再次遞迴，這次是分解成1~2,3~4,5~6以及7~8。

這次3~4和5~6都有被完全包含，因此可以直接回傳這個區間的值。而1~2和7~8還是沒有。所以這兩個區間還要再次向下查詢。

查詢時最重要的是，若區間完全被包含就直接回傳，若完全沒被包含就不往那邊搜尋，否則再將區間分成兩塊向下遞迴。

實作

可以發現他是一顆二元樹，於是我們有兩種做法：指標型與陣列型。以下實作以區間總和為範例。

指標型

請詳讀程式碼，我盡可能詳細註解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include<bits/stdc++.h>
using namespace std;

int n;

struct node{
    //value
    int val;

    //左右子樹的指標
    node *rch,*lch;
    
    //建構式
    node(){
        val=0;
        rch=lch=nullptr;
    }

    //帶有初始值的建構式
    node(int v){
        val=v;
        rch=lch=nullptr;
    }

    //當左右子樹改變時，應重新計算父節點的值
    void pull(){
        //歸零
        val=0;
        //必須先有左右子樹才能拜訪
        //if(l) 相當於 if(l!=nullptr)
        if(lch) val+=lch->val;
        if(rch) val+=rch->val;
    }

    //單點修改
    void modify(int p,int v,int lb=1,int rb=n){
        //終止條件：區間長度為1
        if(lb==rb){
            val=v;
            return;
        }

        //若左右子樹沒有結點則開一個新的
        if(!lch) lch=new node();
        if(!rch) rch=new node();

        //設mid為區間中點，均分為左右區間
        //>>1相當於/2，但快很多
        int mid=lb+rb>>1;

        //左邊走左，右邊走右
        if(p<=mid) lch->modify(p,v, lb ,mid);
        if(mid<p)  rch->modify(p,v,mid+1,rb);

        //還記得子樹修改完要做什麼？
        pull();
    }

    int query(int l,int r,int lb=1,int rb=n){
        //終止條件：所在區間位於欲查詢區間之中
        if(l<=lb && rb<=r){
            return val;
        }

        //同modify
        int mid=lb+rb>>1;

        //左右遞迴求解
        int ret=0;
        //若左右區間不在要查詢的區間或是沒有左右子樹則不遞迴
        if(lch && l<=mid) ret+=lch->query(l,r, lb ,mid);
        if(rch && mid<r)  ret+=rch->query(l,r,mid+1,rb);

        //為求保險，以及供以後懶人標記使用
        pull();

        return ret;
    }
};

node *rt=new node();//root

陣列型

設根節點idx為1，在完滿二元樹中，左子樹就會是\(idx \times 2\)，右子樹就是\(idx \times 2+1\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include<bits/stdc++.h>
using namespace std;

const int N=100010;

int a[N];
//陣列seg的大小建議是N*4，否則你要先知道大於N的最小2^k值
// 131072 -> 262144 所以其實開 262200 就可以了
int seg[N*4];
int n,MXN=1;

//不同於指標型的是：陣列行要預建構
void build(int lb=1,int rb=MXN,int idx=1){
    //終止條件：區間長度為1
    if(lb==rb) return;
    
    //設mid為區間中點，均分為左右區間
    //>>1相當於/2，但稍快
    int mid=lb+rb>>1;
    
    //idx*2   為左子樹
    //idx*2+1 為右子樹
    build(lb,mid,idx*2);
    build(mid+1,rb,idx*2+1);
    
    seg[idx]=seg[idx*2]+seg[idx*2+1];
}

void init(){
    //為了讓他長度為2^k
    while(MXN<n) MXN<<=1;
    //歸零
    for(int i=MXN+1;i<MXN*2;i++) seg[i]=0;
    //以陣列的內容對其初始化
    for(int i=1;i<=n;++i) seg[MXN+i-1]=a[i];
    //將所有節點都建構好
    build();
} 

void modify(int x,int k){
    //此部分也與指標型不同，陣列可以直接依據座標修改
    x=x+MXN-1;
    seg[x]=k;
    
    //向上更新節點
    while(x>1){
        x>>=1;
        seg[x]=seg[x*2]+seg[x*2+1];
    }
}

int query(int l,int r,int lb=1,int rb=MXN,int idx=1){
    //終止條件：所在區間位於欲查詢區間之中
    if(l<=lb && rb<=r) return seg[idx];
    
    //設mid為區間中點，均分為左右區間
    //>>1相當於/2，但稍快
    int mid=lb+rb>>1;

    //左右遞迴求解
    int ret=0;
    
    //若左右區間不在要查詢的區間或是沒有左右子樹則不遞迴
    if(l<=mid)   ret+=query(l,r, lb ,mid,idx*2);
    if(r>=mid+1) ret+=query(l,r,mid+1,rb,idx*2+1);
    
    return ret;
}

int main(){
    ios::sync_with_stdio(0);cin.tie(0);
    
    cin>>n;
    for(int i=1;i<=n;++i) cin>>a[i];
    //一定要記得init()
    init();
}

懶人標記

以上的實作方法都只能用於單點修改，而若需要區間加值的話則會很費時，因此有人想到一個方法：若要修改的區間剛好完全包含線段樹上的某個區間的話，就可以先在上面打一個標記。等到需要動到他下面的子區間再向下放。這樣的話區間加值也可以從 \(O(nlog(n))\) 進步到 \(O(log(n))\) 。

實作

指標型

請詳讀程式碼，我盡可能詳細註解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
#include<bits/stdc++.h>
using namespace std;

int n;

struct node{
    //value tag
    int val,tag;

    //左右子樹的指標
    node *rch,*lch;
    
    //建構式
    node(){
        val=tag=0;
        rch=lch=nullptr;
    }

    //帶有初始值的建構式
    node(int v){
        val=v, tag=0;
        rch=lch=nullptr;
    }

    //多了一個push()，將標記下放
    void push(int l,int r){
        //>>運算會在+-之後
        int len=r-l+1>>1;
        if(lch){
            lch->val+=tag*len;
            lch->tag+=tag;
        }
        
        if(rch){
            rch->val+=tag*len;
            rch->tag+=tag;
        }
        tag=0;
    }
    
    //當左右子樹改變時，應重新計算父節點的值
    void pull(){
        //歸零
        val=0;
        //必須先有左右子樹才能拜訪
        //if(l) 相當於 if(l!=nullptr)
        if(lch) val+=lch->val;
        if(rch) val+=rch->val;
    }

    //單點修改
    void modify(int p,int v,int lb=1,int rb=n){
        //終止條件：區間長度為1
        if(lb==rb){
            val=v;
            return;
        }

        //若左右子樹沒有結點則開一個新的
        if(!lch) lch=new node();
        if(!rch) rch=new node();

        //在遞迴之前先下放標記
        push(lb,rb);
        
        //設mid為區間中點，均分為左右區間
        //>>1相當於/2，但快很多
        int mid=lb+rb>>1;

        //左邊走左，右邊走右
        if(p<=mid) lch->modify(p,v, lb ,mid);
        if(mid<p)  rch->modify(p,v,mid+1,rb);

        //還記得子樹修改完要做什麼？
        pull();
    }

    int query(int l,int r,int lb=1,int rb=n){
        //終止條件：所在區間位於欲查詢區間之中
        if(l<=lb && rb<=r){
            return val;
        }

        //在遞迴之前先下放標記
        push(lb,rb);
        
        //同modify
        int mid=lb+rb>>1;

        //左右遞迴求解
        int ret=0;
        //若左右區間不在要查詢的區間或是沒有左右子樹則不遞迴
        if(lch && l<=mid) ret+=lch->query(l,r, lb ,mid);
        if(rch && mid<r)  ret+=rch->query(l,r,mid+1,rb);

        pull();

        return ret;
    }
    
    //多了一個函式，區間加值
    void add(int l,int r,int v,int lb=1,int rb=n){
        //終止條件：所在區間位於欲查詢區間之中
        if(l<=lb && rb<=r){
            //由於區間為閉區間[lb,rb]因此要加1
            val+=v*(rb-lb+1);
            tag+=v;
            return;
        }

        //在遞迴之前先下放標記
        push(lb,rb);
        
        //同modify
        int mid=lb+rb>>1;

        //左右遞迴求解
        int ret=0;
        //若左右區間不在要查詢的區間或是沒有左右子樹則不遞迴
        if(lch && l<=mid) lch->add(l,r,v, lb ,mid);
        if(rch && mid<r)  rch->add(l,r,v,mid+1,rb);

        //改完不要更新節點
    }
};

node rt;//root

習題

Segment Tree 練習(ZJe409)

題目概述 :

將 \(A[x]\)的值更新為 \(y\)
要查詢 \(A[X]\)~\(A[Y]\) 之中最大值\(maxA\)及最小值\(minA\)的差

輸入說明 :

第1列有兩個正整數 \(k\) \(m\) ，第2列有 \(k\) 個正整數, 請讀入放至 \(A[1..k]\)
接著讀入第3列的 \(N\) \(Q\) 兩個正整數，呼叫所附的產生測資程式 gen_dat()
以上 \(5<k \leq n, 5<m<1000\)
然後就是解題，依\(C,X,Y\)陣列的值 執行更新或查詢

輸出說明 :

若為調查，則輸出區域中的元素總和，若為修改，則不必輸出

範例輸入 1 :

1
2
3
10 541
12 34 56 78 91 23 45 67 89 111
25 15

範例輸出 1 :

1
2
3
4
5
6
7
8
9
328
68
406
0
79
251
327
489
0

戰術資料庫(110宜中資訊社校內賽pF)

題目敘述 :

要求能在一個陣列中做以下操作

  1. 搜尋區間和 \(find sum\) \((l)\) \((r)\)
  2. 搜尋區間最大和最小值 \(find\) \(max/min (l)\) \((r)\)
  3. 單點加減值 \(plus/minus\) \((position)\) \((k)\)

輸入說明 :

輸入第一行有一個數字 n, q ，下一行有 n 個數字，緊接著有 q 筆操作，可能為以下五種

  1. 搜尋區間和
  2. 搜尋區間最大和最小值
  3. 單點加減值

相鄰數字間以空白隔開。
\(n, q \leq 100000 , a[i] \leq 100000\)

輸出說明 :

對於每個搜尋指令做出回答

範例輸入 1 :

1
2
3
4
5
6
7
8
9
10
11
12
7 10
1 2 3 4 5 6 7
find max 2 5
find min 1 4
minus 3 1
plus 2 4
find sum 1 7
plus 7 -3
find sum 1 3
minus 6 0
plus 1 1
find max 1 7

範例輸出 1 :

1
2
3
4
5
5
1
31
9
6

2022/1/10

樹堆(Treap)

Treap 是一個隨機平衡的二元搜尋樹，這裡所說的 Treap 是以 merge/split 的方式實作的，這樣實作的 Treap 有很多好處，我們先說明他的基本規則，以及 merge/split 函式(function)在做什麼，結著說明如何實作。

樹堆的名稱來由是 樹(Tree) 和 堆積(Heap) 結合而成，每個節點會至少存放兩個數值 val,pri ， val (也有人叫他 key)就是內容，而 pri 則是用以平衡。

規則與前置作業

  • 所有節點的 pri 值必須比他的左右子樹小(大也可以)
  • 樹上的 val 滿足 \(“二元搜尋樹”\) 的性質

為了避免有人忘記什麼是 \(“二元搜尋樹”\) 的性質，以下用一個我出過的題目說明。

Safe Sorter

pic
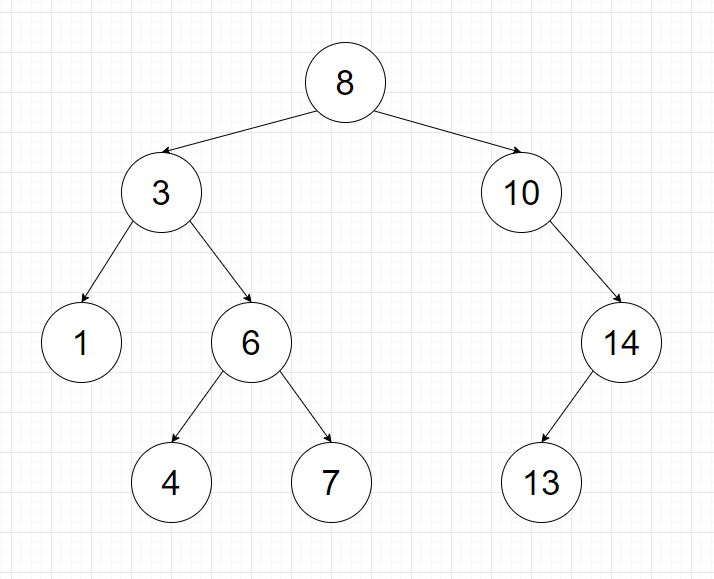
  • 如果該節點還沒有任何保險箱，此保險箱就會佔據該節點
  • 否則若這個要放入的保險箱裡面的金塊比在該節點的保險箱還要多，他會被往右邊送
  • 否則就往左邊送
  • 必須送到他占用一個節點為止

以上圖為例

  • 第一個放進來的保險箱有 8 個金塊
  • 第二個有 10 個，因此他被放在右邊
  • 第三個有 14 個，因此第一步會先往右送，發現右邊的節點也有保險箱了，因而再次被往右送
  • 第四個有 3 個，於是被放在左邊
  • 其他依此類推

而所謂隨機平衡就是他的平衡方式來自所有節點被賦予的一個隨機的 pri 值。

Treap 當中最重要的就是以下兩種操作

  • merge(a,b) : 將兩顆樹 a, b 合併。前提 : a, b 滿足所有在 a 裡面的節點所存放的值皆小於所有在 b 裡面的節點
  • split(a,b,p) : 將一棵樹分成 a, b 並同時滿足 a 中的值皆小於等於 \((\le)\) p ， 而 b 中的值皆大於 \((>)\) p

兩者詳細步驟是依照遞迴定義的，如下。

Merge

  • 如果 a,b 至少其中一個是空指標，回傳非空的那一個 (兩個都空救回傳空指標)
  • 否則為了同時維持 BST 和 heap 的性質，我們先判斷哪一個的 pri(priority) 值更大，我的實作是將 pri 值小的放上面 (較接近樹根的位置)
  • 如果 a 的 pri 值較小，我們會回傳 a 作為呼叫此函數的樹的根，不過在此之前，我們要先決定 a 的右子樹 (因為 b 也還沒被合併完) ，所以要向下遞迴
  • b 的情況剛好相反，因為 b 裡面的值都大於 a 裡面的值

實作

1
2
3
4
5
6
7
8
9
10
11
node *merge(node *a,node *b){
    if(!a || !b) return a ? a : b;

    if(a->pri < b->pri){
        a->rch=merge(a->rch,b);
        return a;
    }else{
        b->lch=merge(a,b->lch);
        return b;
    }
}

Split

split 較為複雜，因為同時要滿足 Treap 的兩種性質

  • 若 T(要被分割的 Treap) 為空指標的話，代表整棵樹都被分完了，因此將 a,b 都設為空指標。
  • 否則一樣要分成兩個條件 : T 的根結點的值小於等於 p ，和大於 p
  • 如果 T 的根結點的值小於等於 p ，選擇將 T 的根結點與他的左子樹給 a 並繼續向下分解 T 的右子樹給 a 的右子樹與 b
  • 否則將 T 的根結點與他的右子樹給 b 並繼續向下分解 T 的左子樹給 b 的左子樹與 a

實作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void split(node *T,node *&a,node *&b,int p){
    if(!T){
        a=b=nullptr;
        return;
    }
    
    if(T->key <= p){
        a=T;
        split(T->rch,a->rch,b,p);
    }else{
        b=T;
        split(T->lch,a,b->lch,p);
    }
}

名次樹

首先介紹一下名次樹，名次樹是透過在節點內多存一個數值 \(\to\) 子樹大小(size)，以實現更多功能，例如 : k 在這棵樹裡面排第幾，刪除比 k 大的第一個數，還有排名第 k 的樹為何等。

為了在 Treap 中實現這個功能，我們要多實作兩個函數 \(\to\) pull & SplitBySize(splitSz)。

首先，我先將節點完整的 struct ，還有尋找某個指標底下的樹的 size 的函式寫出來，方便後續講解。順帶一題，為了維持名次樹的正確性，每次只要樹有經過更動就要 執行 pull 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
struct node{
    // key 是排序依據
    // pri 是 heap 的依據
    int key,pri,sz;
    node *lch,*rch;
    
    node(int _key){
        key=_key;
        sz=1;
        lch=rch=nullptr;
        // RandomInt() 之後會實作
        pri=RandomInt();
    }
    
    void pull(){
        // 自己也算
        sz=1;
        // 判斷式相當於 lch!=nullptr
        // 要加上左右子樹的大小才是完整的
        if(lch) sz+=lch->sz;
        if(rch) sz+=rch->sz;
    }
};

int fs(node *a){
    // 如果 a 為空指標則 sz(回傳值) 為 0
    return a ? a->sz : 0;
}

SplitBySize

這個函式會與 Split 有點像，差別在於分開的依據不同， SplitBySize 會將整棵樹分為 a, b ， 其中 a 存有前 s 小的所有數， b 則存剩下的。詳細步驟如下。

  • 與 Split 相同，若 T 為空則表示分完，將 a,b 都設為空指標
  • 否則如果 T 的左子樹的元素個數不到 s ，將 T 和他的左子樹都給 a ，然後繼續從 T 的右子樹當中切出 s-( T 的左子樹大小)-1( T 自己) 個元素給 a 的右子樹
  • 否則將 T 和他的右子樹都給 b ，然後從 T 的左子樹當中切出 s 個元素給 a

實作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void splitSz(node *T,node *&a,node *&b,int s){
    if(!T){
        a=b=nullptr;
        return;
    }

    if(fs(T->lch)<s){
        a=T;
        splitSz(T->rch,a->rch,b,s-fs(T->lch)-1);
        // 普通的 Split 中放 pull 的位置與他相同
        a->pull();
    }else{
        b=T;
        splitSz(T->lch,a,b->lch,s);
        b->pull();
    }
}

隨機數

C++ 本身就有內建隨機函式可供取用。就直接放在下面供大家參考。

1
2
3
4
5
6
// 簡單作法，但可能被 hack
#include<crand>

int RandomInt(){
    return rand();
}
1
2
3
4
5
6
7
8
9
// 較長，但較不易被破解
#include<random>

unsigned seed=chrono::steady_clock().now().time_since_epoch().count();
mt19937 rng(seed);

int RandomInt(){
    return rng();
}

基本功能

有了這些函式之後，後面的大多數操作都會變很簡單，舉凡插入(insert)，刪除(erase)，尋找(find) 等等。因為他們都可以用 merge and split 湊出來。而且很多功能甚至不只有一種實作方法。讓我們看下去。

Insert

insert 可以被簡單地分成幾個步驟。假設我要插入的數字為 v 。

  • 將整棵樹(我都存在 rt 指標中) 切成小於等於 v 和大於 v 的兩棵樹 rt, b
  • 另外用 v new 一個節點 a(v) 出來 (不會動態記憶體分配的可以先去複習一下)。
  • 合併 rt 和 a ，並將合併後的樹給 rt
  • 合並 rt 和 b ，並將合併後的樹給 rt

實作

1
2
3
4
5
6
void insert(int v){
    node *a=new node(v),*b;
    split(rt,rt,b,v);
    rt=merge(rt,a);
    rt=merge(rt,b);
}

Erase

Erase 一樣可以被簡單地分成幾個步驟。假設我要刪除的數字為 v 。

1. 刪除所有等於 v 的數(整數才可以)

  • 將整棵樹(我都存在 rt 指標中) 切成小於等於 v 和大於 v 的兩棵樹 rt, b
  • 再將 rt 指向的樹切成小於等於 v-1 和大於 v-1 的兩棵樹 rt, a
  • 刪除 a 整棵樹
  • 合併 rt 和 b ，並將合併後的樹給 rt

2. 刪除一個等於 v 的數(整數才可以)

  • 將整棵樹(我都存在 rt 指標中) 切成小於等於 v-1 和大於 v-1 的兩棵樹 rt, b
  • 再將 b 指向的樹切成左邊一個元素，剩下都放右邊的 b, a
  • 刪除 b
  • 合併 rt 和 b ，並將合併後的樹給 rt

實作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// 這個函式是先刪除左右子樹，再刪除自己，並透過遞迴來刪掉整棵樹。
void delete_tree(node *n){
    if(n->lch) delete_tree(n->lch);
    if(n->rch) delete_tree(n->rch);
    delete(n);
}

// erase all element between (v-1~v] -> 對應 1
void erase(int v){
    node *a,*b;
    split(rt,rt,b,v);
    split(rt,rt,a,v-1);// or v-eps
    // it's better to use delete_tree function
    delete(a);
    rt=merge(rt,b);
}

// erase one element between (v-1~v] -> 對應 2
void erase(int v){
    node *a,*b;
    split(rt,rt,b,v-1);
    splitSz(b,b,a,1);
    delete(b);
    rt=merge(rt,b);
}

Count

Count 還是可以被簡單地分成幾個步驟。假設我要數的數字為 v 。

  • 將整棵樹(我都存在 rt 指標中) 切成小於等於 v 和大於 v 的兩棵樹 rt, b
  • 再將 rt 指向的樹切成小於等於 v-1 和大於 v-1 的兩棵樹 rt, a
  • 用一個變數將 a 的 size 存起來
  • 合併 rt 和 a ，並將合併後的樹給 rt
  • 合併 rt 和 b ，並將合併後的樹給 rt

實作

1
2
3
4
5
6
7
8
9
int count(int v){
    node *a,*b;
    split(rt,rt,b,v);
    split(rt,rt,a,v-1);// or v-eps
    int ret=fs(a);
    rt=merge(rt,a);
    rt=merge(rt,b);
    return ret;
}

Kth Small Element

假設我要找第 p 小的數字。

  • 將整棵樹(我都存在 rt 指標中) 切成左邊 p 個元素，剩下都放右邊的 rt, b
  • 再將 rt 指向的樹切成左邊 p-1 個元素，剩下都放右邊的 rt, a
  • 用一個變數將 a 的值存起來
  • 合併 rt 和 a ，並將合併後的樹給 rt
  • 合併 rt 和 b ，並將合併後的樹給 rt

實作

1
2
3
4
5
6
7
8
9
int kth(int v){
    node *a,*b;
    splitSz(rt,rt,b,p);
    splitSz(rt,rt,a,p-1);
    int ret=a->key;
    rt=merge(rt,a);
    rt=merge(rt,b);
    return ret;
}

你以為只是平衡樹嗎？不不不，祂可厲害了

進階功能

如果我們將整棵樹的中序遍歷當成序列的順序的話(如下圖)，我們可以實現需多更強大的功能。可以說，線段樹能做到的事 Treap 都可以做到，但 Treap 甚至可以做到許多線段樹做不到的事。

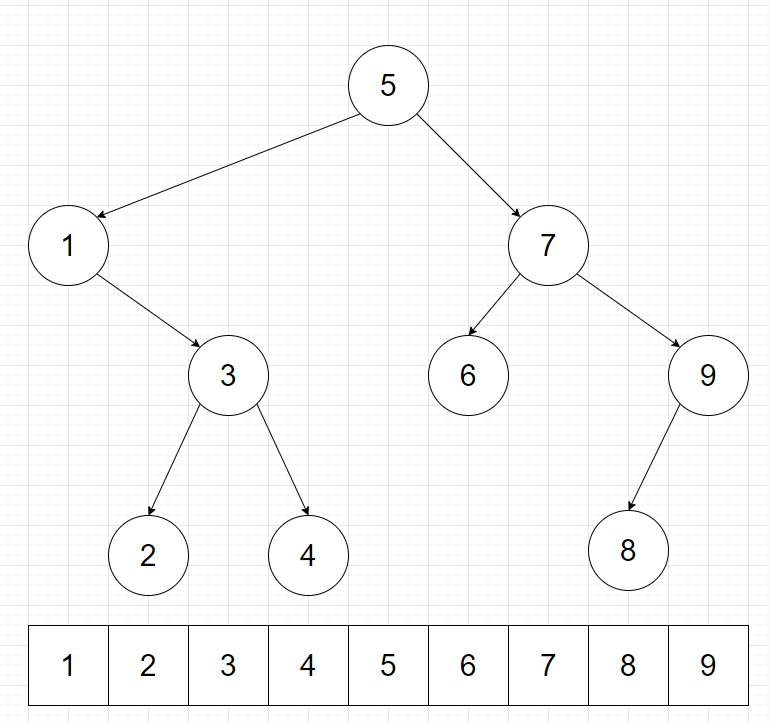
Treap

而且，此時我們可以把 key 拔掉。然後只使用 splitSz 和 merge 。

Insert

假設我希望插入的數字位於第 p 個，且值為 v 。

  • 將整棵樹(我都存在 rt 指標中) 切 p-1 個給 rt ，其他剩下的分給 b
  • 另外用 v new 一個節點 a(v) 出來
  • 合併 rt 和 a ，並將合併後的樹給 rt
  • 合並 rt 和 b ，並將合併後的樹給 rt

實作

1
2
3
4
5
6
void insert(int p,int v){
    node *a=new node(v),*b;
    splitSz(rt,rt,b,p-1);
    rt=merge(rt,a);
    rt=merge(rt,b);
}

Erase

假設我要刪除第 p 個數

  • 將整棵樹(我都存在 rt 指標中) 切 p-1 個給 rt ，其他給 b
  • 再將 b 指向的樹切一個給 b 剩下給 a
  • 刪除 a
  • 合併 rt 和 b ，並將合併後的樹給 rt

實作

1
2
3
4
5
6
7
void erase(int p){
    node *a,*b;
    splitSz(rt,rt,b,p-1);
    splitSz(b,b,a,1);
    delete(b);
    rt=merge(rt,b);
}

區間操作

在介紹區間操作之前，我們還需要在節點上加入更多的資訊和函式，所以 node 裡面會有更多程式碼。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
const int INF=0x3f3f3f3f

struct Treap{
    struct node{
        // 此節點的值
        int val;
        // 維持 Treap 的性質
        int pri,sz;
        // 用在區間查詢
        int sum,mx,mn;
        // 可以支援區間反轉
        bool rev_tag;
        // 可以支援區間加值
        int add_tag;
        // 左右子樹
        node *lch,*rch;
        
        node(int _val){
            val=sum=mx=mn=_val;
            lch=rch=nullptr;
            sz=1;
            pri=rng();
        }
        
        void pull(){
            sz=1;
            sum=mx=mn=val;
            
            if(lch){
                sz+=lch->sz;
                sum+=lch->sum;
                mx=max(mx,lch->mx);
                mn=min(mn,lch->mn);
            }
            
            if(rch){
                sz+=rch->sz;
                sum+=rch->sum;
                mx=max(mx,rch->mx);
                mn=min(mn,rch->mn);
            }
        }
        
        // 讓他底下的區間都反轉
        void rev(){
            rev_tag=!rev_tag;
        }
        
        // 再更改節點前用
        void push(){
            if(rev_tag){
                swap(lch,rch);
                if(lch)
                    lch->tag=true;
                if(rch)
                    rch->tag=true;
            }
            
            if(lch)
                lch->add_tag+=add_tag;
            if(rch)
                rch->add_tag+=add_tag;
            add_tag=0;
        }
    };
};

同時，我們在原來的 merge/split 操作程式碼中，都要加上 push ，具體位置如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
struct Treap{
    node *merge(node *a,node *b){
        if(!a || !b) return a ? a : b;

        if(a->pri < b->pri){
            a->push();
            a->rch=merge(a->rch,b);
            return a;
        }else{
            b->push();
            b->lch=merge(a,b->lch);
            return b;
        }
    }
    
    void splitSz(node *T,node *&a,node *&b,int s){
        if(!T){
            a=b=nullptr;
            return;
        }

        T->push();
        
        if(fs(T->lch)<s){
            a=T;
            splitSz(T->rch,a->rch,b,s-fs(T->lch)-1);
            a->pull();
        }else{
            b=T;
            splitSz(T->lch,a,b->lch,s);
            b->pull();
        }
    }
};

接下來的操作都是把區間切下來，做完我要做的事，再接回去就可以了。

區間查詢(極值、總和)

假設現在要查詢 l~r 的區間

  • 從 rt 切下 r 個節點給 rt ，其它給 b
  • 接著從 rt 切下 l-1 個節點給 rt ，其餘給 a
  • 此時 a 就存有區間 \([ ; l, , r ; ]\) ，而他上面的 sum, mx, mn 就會是這個區間的總和、最大值，以及最小值
  • 最後先按照順序把它合併，再回傳答案即可

實作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int query(int l,int r){
    node *a,*b;
    splitSz(rt,rt,b,r);
    splitSz(rt,rt,a,l-1);
    // 下一行放 sum, mx, mn 看需求
    int ret=a->sum;
    rt=merge(rt,a);
    rt=merge(rt,b);
    return ret;
}

// 單點查詢就用查詢長度為 1 的區間重復利用函式就可以了
int get(int p){
    return query(p,p); 
}

單點修改

先將所要修改的位置切下來，在修改完後記得要 push 。

1
2
3
4
5
6
7
8
void modify(int p,int v){
    node *a,*b;
    splitSz(rt,rt,a,p-1);
    splitSz(a,a,b,1);
    a->val=v;
    rt=merge(rt,a);
    rt=merge(rt,b);
}

區間操作

假設現在要對 l~r 的區間進行操作

  • 從 rt 切下 r 個節點給 rt ，其它給 b
  • 接著從 rt 切下 l-1 個節點給 rt ，其餘給 a
  • 此時 a 就存有區間 \([ ; l, , r ; ]\) ，直接對他操作就可以了
  • 最後先按照順序把它合併

實作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 區間反轉
void reverse(int l,int r){
    node *a,*b;
    splitSz(rt,rt,b,r);
    splitSz(rt,rt,a,l-1);
    if(a) a->rev();
    rt=merge(rt,a);
    rt=merge(rt,b);
}

// 區間加值
void add(int l,int r,int v){
    node *a,*b;
    splitSz(rt,rt,b,r);
    splitSz(rt,rt,a,l-1);
    a->val+=v;
    a->push();
    rt=merge(rt,a);
    rt=merge(rt,b);
}

特殊功能

Count \([ ; l, , r ; ]\)

在一棵作為二元搜尋樹的 Treap 中，計算介於 l 到 r 的元素數量

基本上就跟上面區間查詢相同。只是切割依據不同。

實作

1
2
3
4
5
6
7
8
9
10
int count(int l,int r){
    node *a,*b;
    split(rt,rt,b,r);
    split(rt,rt,a,l-1);
    // 下一行依據要插尋的內容放 sz(數量) 或 sum(總和)
    int ret=a->sz;
    rt=merge(rt,a);
    rt=merge(rt,b);
    return ret;
}

Sum \([ ; l, , r ; ]\) (rank)

在一棵作為二元搜尋樹的 Treap 中，計算介於第 l 小到第 r 小的元素總和

同樣就跟上面區間查詢相同。只是元素排列方式不同。

實作

1
2
3
4
5
6
7
8
9
10
int Sum(int l,int r){
    node *a,*b;
    splitSz(rt,rt,b,r);
    splitSz(rt,rt,a,l-1);
    // 下一行依據要插尋的內容放 sum(總和) 或 xor 值
    int ret=a->sum;
    rt=merge(rt,a);
    rt=merge(rt,b);
    return ret;
}

解構式

對於多筆測資，可能會需要釋放記憶體。由於 Treap 二元樹的特性，可以透過遞迴刪除整棵樹

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
struct Treap{
    struct node{
        int val;
        node *lch,*rch;
    }
    
    node *rt=nullptr;
    
    void DeleteTree(node *n){
        if(n->lch) DeleteTree(n->lch);
        if(n->rch) DeleteTree(n->rch);
        delete(n);
    }
    
    ~Treap(){
        if(rt) DeleteTree(n);
    }
}

重載輸入輸出

要前中後序都可以

1
2
3
4
5
6
7
8
9
10
11
12
void print(node *n,ostream &output){
    n->push();
    if(n->lch) print(n->lch,output);
    // 下面這一行放的位置會決定他是前中後序
    output<<n->val<<" ";
    if(n->rch) print(n->rch,output);
}

friend ostream &operator<<(ostream &output,PowerfulArray &a){
    a.print(a.rt,output);
    return output;
}

一些 STL 的常見函式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
int size(){
    return fs(rt);
}

bool empty(){
    return size()==0;
}

void push_back(num v){
    insert(size()+1,v);
}

void push_front(num v){
    insert(1,v);
}

void pop_back(){
    erase(size()+1);
}

void pop_front(){
    erase(1);
}

void resize(int sz){
    while(size()<sz){
        push_back(0);
    }
    while(size()>sz){
        pop_back();
    }
}

void resize(int sz,num v){
    while(size()<sz){
        push_back(v);
    }
    while(size()>sz){
        pop_back();
    }
}

建構式

有了上述的 STL 常見函式之後，就可以很方便的寫建構式了。

1
2
3
4
5
6
7
8
Treap(){ }
Treap(int sz){
    resize(sz);
}

Treap(int sz,int v){
    resize(sz,v);
}